limita
Matematická analýza
[Latina], základní pojem matematické analýzy. Intuitivně znamená hodnotu, k níž se nějaká (proměnná) veličina neomezeně blíží. Pomocí pojmu limita se definují další základní pojmy matematické analýzy, například derivace, integrál, desetinný rozvoj reálného čísla ap.
Limitní funkce f v bodě a je číslo L:
\( L = \lim\limits_{x \to a} f(x) \),
pro které platí:
ke každému kládnému číslu ε existuje takové kladné číslo δ, že \[ |f(x) - L| < \varepsilon \text{ pro všechna } x \text{ splňující } 0 < |x - a| < \delta. \]
To je exaktní formulace intuitivní představy: je-li x velmi blízko čísla a, je f(x) velmi blízko číslu L. Z matematického hlediska je důležité, že hodnota f(a) v definici nevystupuje a nemusí být vůbec definována.
Například platí:
\[ \lim\limits_{x \to 0} \frac{\sin x}{x} = 1, \]
ačkoliv hodnota \(\frac {\sin 0} {0}\) není definována. Obdobně se definuje limita zprava (zleva) funkce f v bodě a; přitom místo nerovnosti 0 < |x – a| < δ vystupuje v definici nerovnost 0 < |x – a| < δ (0 < a-x δ), tj. berou se v úvahu jen body x vpravo (vlevo) od a.
Limitní funkce f v bodě \( +\infty \) nebo \( -\infty \) je číslo L, k němuž se blíží hodnota f(x), jestliže x neomezeně roste (klesá); zapisuje se
\( L = \lim\limits_{x \to +\infty} f(x) \) nebo \( L = \lim\limits_{x \to -\infty} f(x) \).
Například:
\[ \lim\limits_{x \to +\infty} \arctan x = \frac{\pi}{2}, \quad \lim\limits_{x \to -\infty} \frac{x}{1 - x} = 1. \]
Uvedené limity se někdy obšírněji nazývají vlastní limity. Jestliže hodnota f(x) neomezeně roste (klesá), když x se blíží k číslu a, říká se, že funkce f má v bodě a nevlastní limitu \( +\infty \) (nebo \( -\infty \)), a píše se:
\[ \lim\limits_{x \to a} f(x) = +\infty \quad (\text{nebo} \; \lim\limits_{x \to a} f(x) = -\infty). \]
Například:
\[ \lim\limits_{x \to 0} \frac{1}{x^2} = \infty, \quad \lim\limits_{x \to \frac{\pi}{2}} |\tan x| = +\infty. \]
Limita posloupnosti a1, a2, ..., an, ... je číslo a, pro které platí: ke každému kladnému číslu ε existuje takové přirozené číslo n0, že pro všechna přirozená čísla n, n ≥ n0, platí nerovnost |an – a| ≤ ε.
Píše se \( \lim\limits_{n \to \infty} a_n = a \), popřípadě stručně \( a_n \to a \). Například:
\[ \lim\limits_{n \to \infty} \frac{1}{n} \sin n = 0, \quad \lim\limits_{n \to \infty} \left( 1 + \frac{1}{n} \right)^n = e. \]
Posloupnost a1, a2, ..., an, ... má nevlastní limitu \( +\infty \) (nebo \( -\infty \)), jestliže čísla an se s rostoucím n neomezeně zvětšují (zmenšují). Například:
\[ \lim\limits_{n \to \infty} (n + (-1)^n) = +\infty. \]
Tento příklad ukazuje, že zvětšování či zmenšování nemusí být monotónní. V moderní matematice se pojem limita rozšiřuje na obecnější matematické objekty (např. limita zobrazení, limita posloupnosti funkcí) a jeho definice se různým způsobem modifikuje (např. stejnoměrná limita, slabá limita).
Vytvořeno:
14. 3. 2000
Aktualizováno:
2. 11. 2024
Autor: -red-
Odkazující hesla: číselná posloupnost, matematická analýza.
Vyzkoušejte si s přáteli Kvízy encyklopedie CoJeCo.cz!
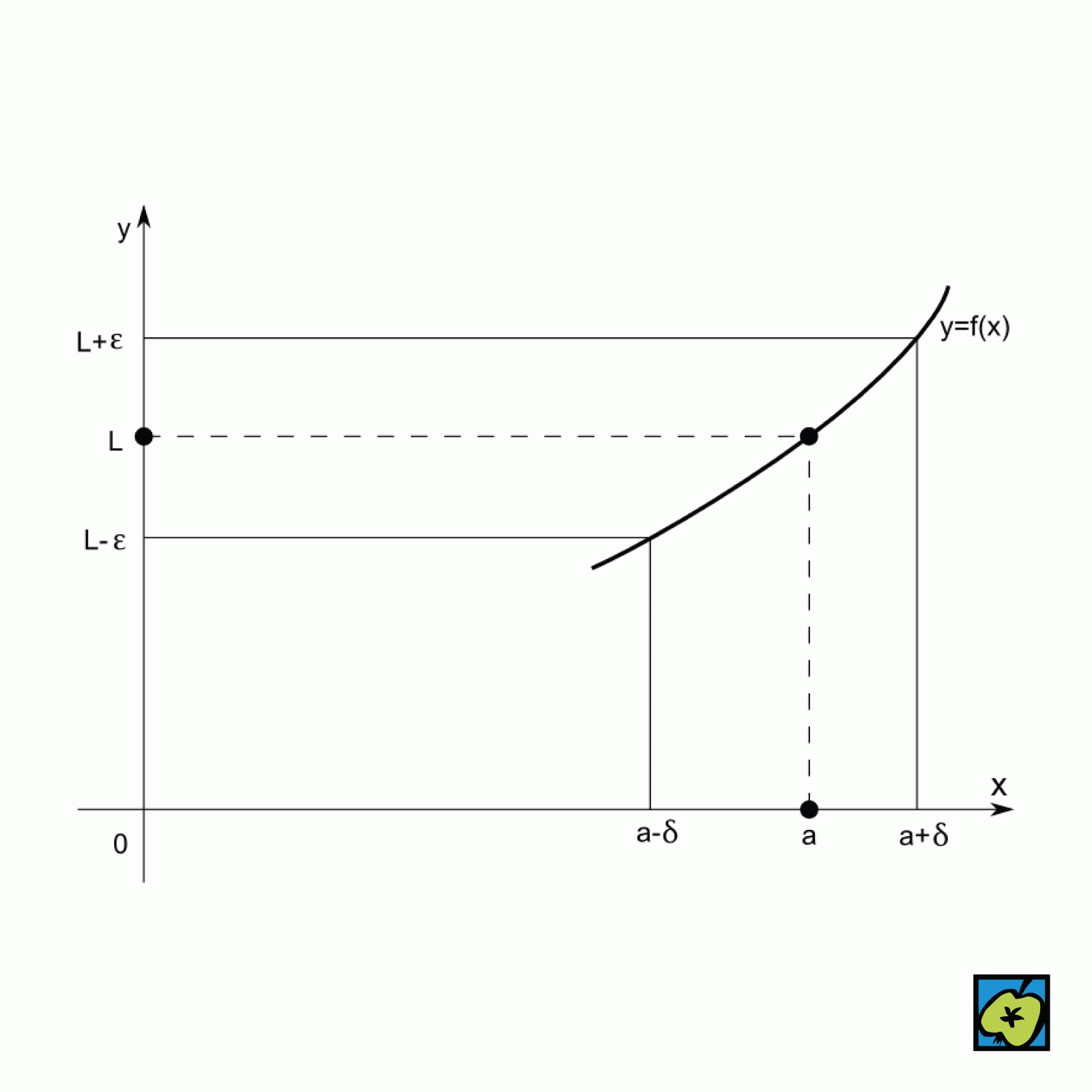
Limita: k definici limity funkce – znázornění funkce y = f(x), která se při hodnotách x dostatečně blízkých bodu a (v intervalu (a−δ, a+δ)) dostává do libovolně zvoleného okolí hodnoty L, například do pásu (L−ε, L+ε). Tím je vyjádřeno, že limita funkce f(x) pro x → a je rovna L. – CoJeCo.cz (CC BY-SA 4.0)
