logaritmus

Matematika / Algebra

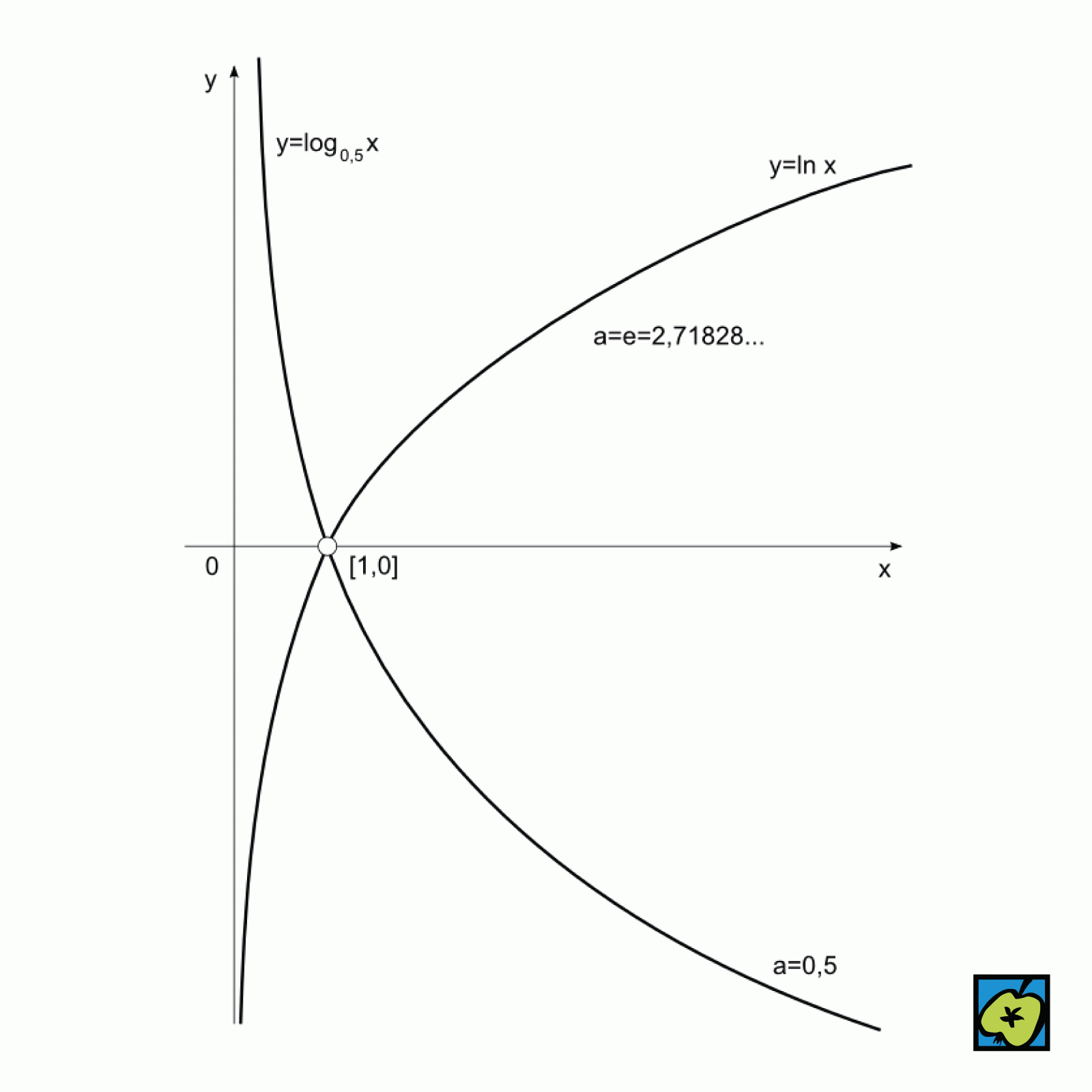
[Řečtina], postup, umožňující nahradit některé složitější početní úkony jednoduššími. Je-li \(a \space \rlap {=} \space {\vert} \space \space0,1 \) a \(x > 0\), pak číslo \(y\)  je logaritmus o základu \(a\)  čísla \(x\) \((y=log_a x)\), platí-li \(a^y=x\) . Dekadický (Briggsův) logaritmus je logaritmus o základu 10 (matematická značka \(log\)), logaritmus, jehož základ je Eulerovo číslo \(e\), se nazývá přirozený (Napierův) logaritmus, matematická značka \(ln\) nebo \(lg\). Pro logaritmy platí:

je-li  \(p,q >0\), \(a \neq 0,1\),  pak

\(log_a(p.q)=log_a p + log_a q\) ,

\(log_a \frac {p}{q} = log_a p - log_a q\) ,

\(log_a(p^\alpha) = \alpha . log_a p\) ,

\(log_a 1 = 0\) .

Každému \(x>0\)  lze jednoznačně přiřadit celé číslo \(c\) a číslo \(m\), \(0 \leq m < 1\) tak, že  \(log \space x = c + m\) . Číslo \(c\) udává řád první nenulové číslice čísla \(x\)  a nazývá se charakteristika \(log \space x\), číslo \(m\) se nazývá mantisa \(log \space x\). Dekadické logaritmy všech čísel, jež se liší jen umístěním desetinné čárky, mají touž mantisu (např. 10² = 100, 10³ = 1000 a tudíž \(log \space 100 = 2\), \(log \space 1000 = 3\), charakteristika \(log \space 100 = 2\), charakteristika \(log \space 1000 = 3\) a mantisa v obou případech je rovna 0). Mantisy logaritmů zaokrouhlené na určitý počet platných číslic bývaly před nástupem kapecních kalkulátorů a počítačů tabelovány v logaritmických tabulkách. Funkce, přiřazující číslo \(log_ax\) se nazývá logaritmická funkce a je inverzní k funkci \(a^x\). Pojem logaritmické funkce a logaritmu se zavádí také pro komplexní čísla. \(a \space \rlap {=} \space {\vert} \space \space0,1 \)

Vytvořeno: 14. 3. 2000
Aktualizováno: 22. 6. 2022
Autor: -red-

Odkazující hesla: John Napier, logaritmické tabulky, mantisa, optická hustota.