kuželosečka

Geometrie

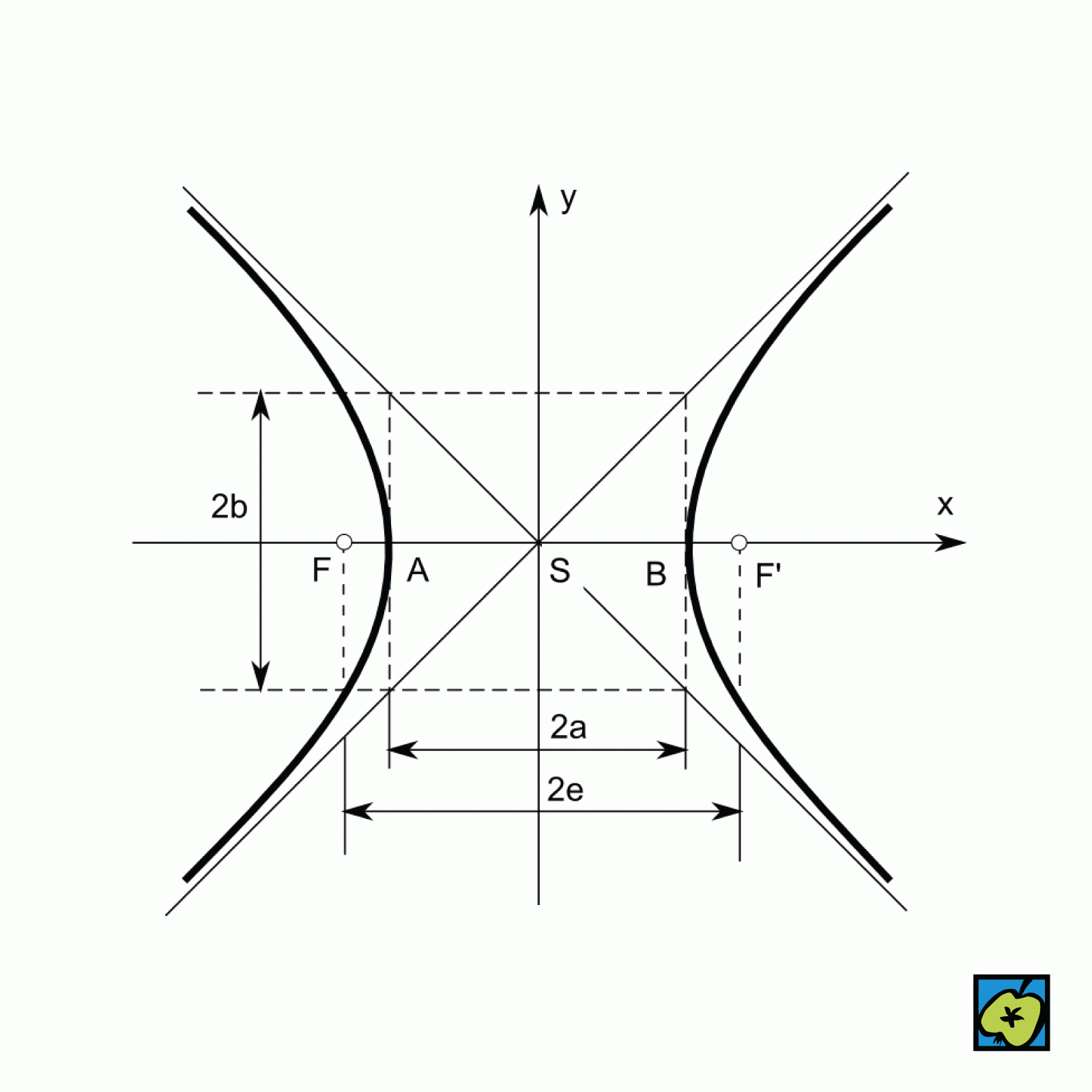
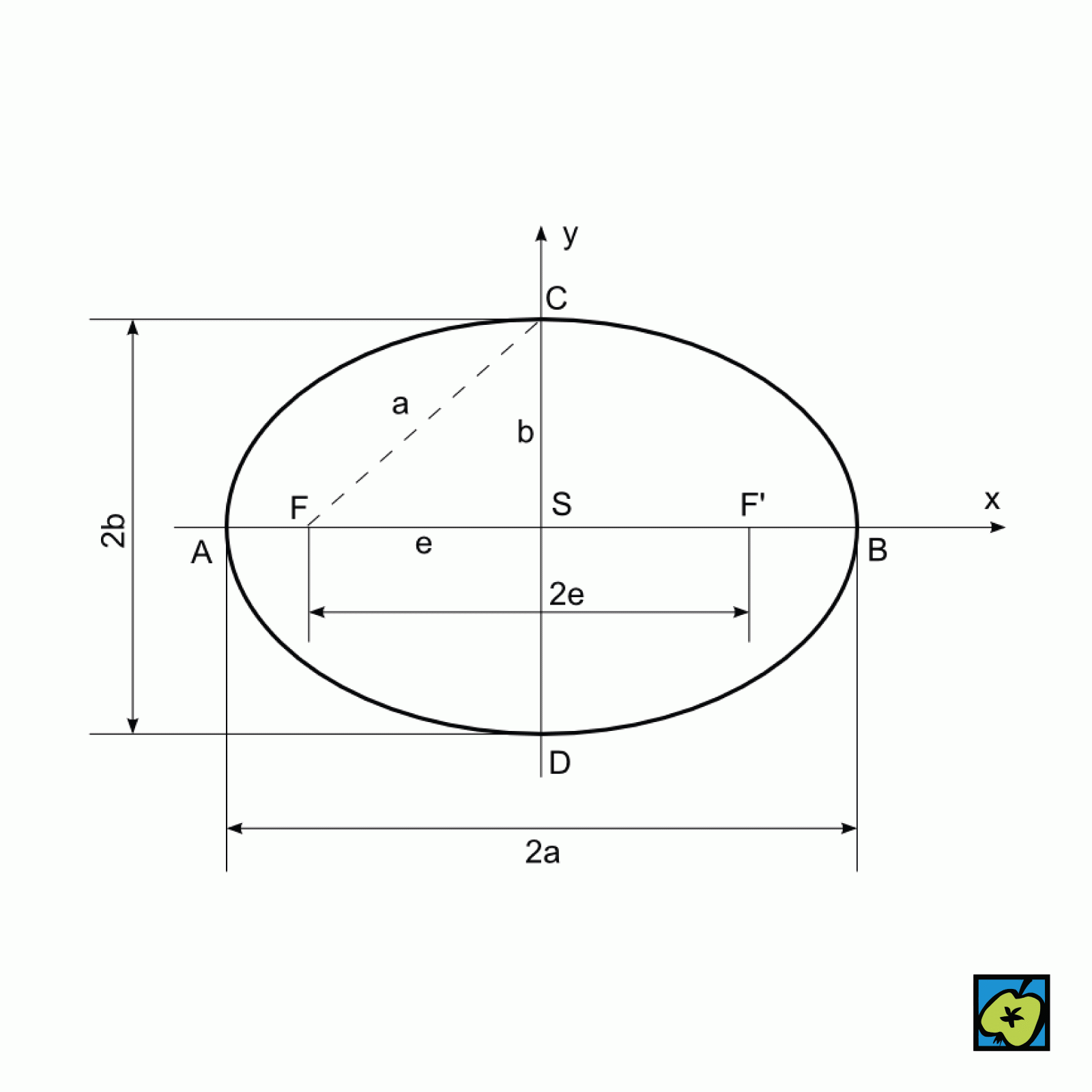
Rovinná křivka vytvořená jako průnik rotační kuželové plochy s rovinou neprocházející jejím vrcholem. Existují tři druhy kuželoseček: elipsa (ve zvláštním případě kružnice), hyperbola, parabola. Jejich analytické vyjádření v pravoúhlých kartézských souřadnicích je

\(\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1\) (elipsa),

\(\frac{x^2}{a^2} - \frac{y^2}{b^2} = 1\) (hyperbola),

\(y^2 = 2px\) (parabola),

a, b délky poloos; p, respektive 2p (p > 0) poloparametr, respektive parametr paraboly.

Vytvořeno: 6. 9. 2006
Aktualizováno: 7. 8. 2024
Autor: -red-

Odkazující hesla: řez.