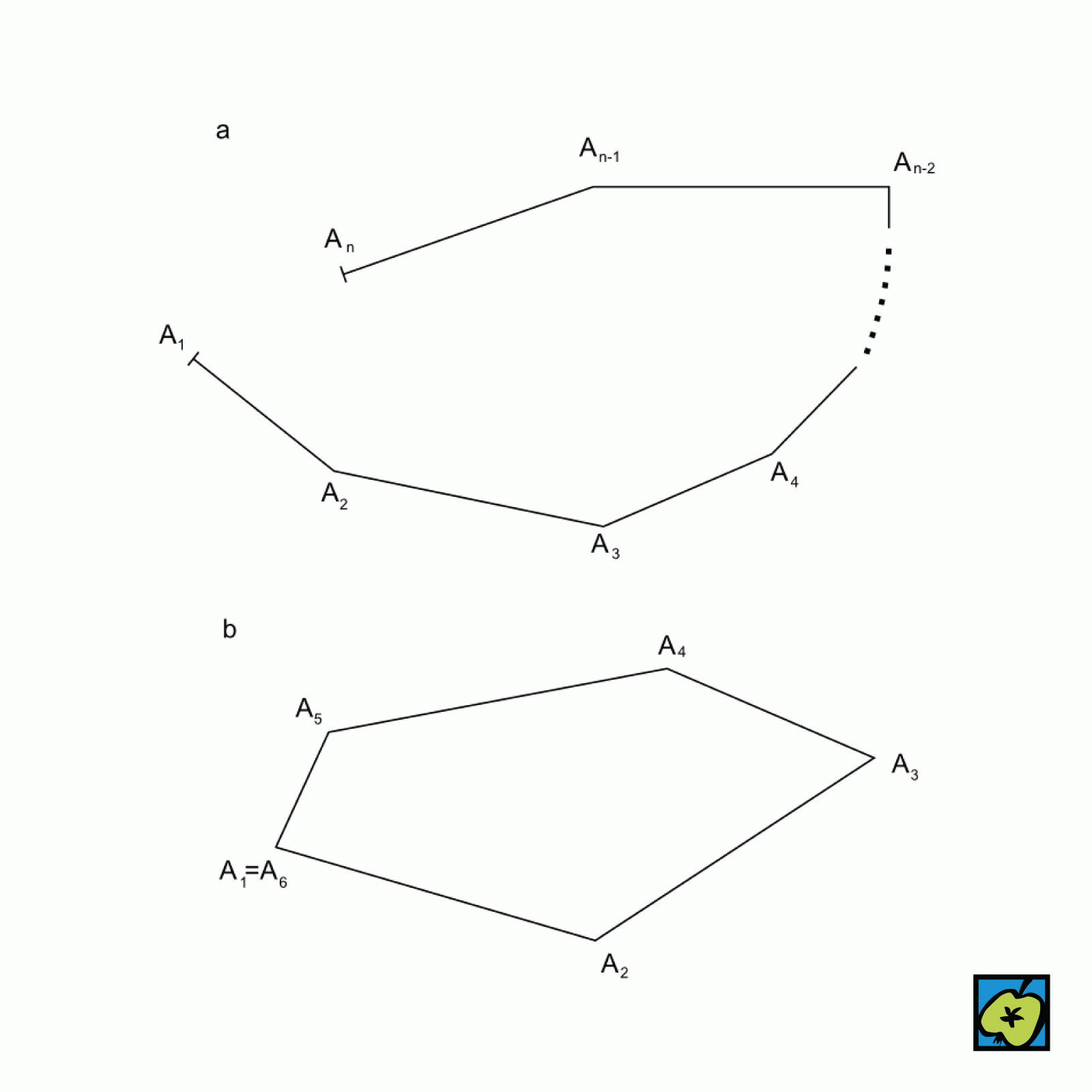
křivka

Matematika / Geometrie

Matematicky jednorozměrná varieta nebo též jednorozměrné kontinuum. Rozlišují se křivky rovinné, prostorové, křivky na ploše a podobně. Křivka v parametrickém tvaru, například v prostoru, je množina bodů, jejichž pravoúhlé kartézské souřadnice x(t), y(t), z(t) jsou spojité funkce proměnné t, probíhající daný interval. Splývají-li body odpovídající krajním bodům tohoto intervalu, nazývá se křivka zavřená (uzavřená). Zavřená křivka je jednoduchá, odpovídají-li (s výjimkou dvojice krajních bodů) všem dvojicím různých bodů intervalu různé body (křivka tedy sama sebe neprotíná). Rovinnou křivkou lze zpravidla popsat jako množinu bodů, jejichž pravoúhlé kartézské souřadnice x, y splňují vztah y = f(x) (explicitní tvar) nebo g(x, y) = 0 (implicitní tvar), kde f, g jsou spojité funkce. Obdobně lze prostorovou křivku zpravidla vyjádřit dvěma rovnicemi. Algebraická křivka je křivka, jejíž rovnice je h(x, y) = 0, kde h(x, y) je mnohočlen. Jednoduchá zavřená křivka v rovině se také nazývá Jordanova křivka. Například kružnice, elipsa, obvod trojúhelníku jsou Jordanovy křivky.

Vytvořeno: 14. 3. 2000
Aktualizováno: 8. 8. 2024
Autor: -red-

Odkazující hesla: přechodnice.