integrální počet

Matematická analýza

Obor matematické analýzy, zabývající se integrály a jejich aplikacemi. Hlavním cílem je vyjádřit kumulativní změny, plochy a objemy. Má široké využití v matematice, fyzice, inženýrství a ekonomii.

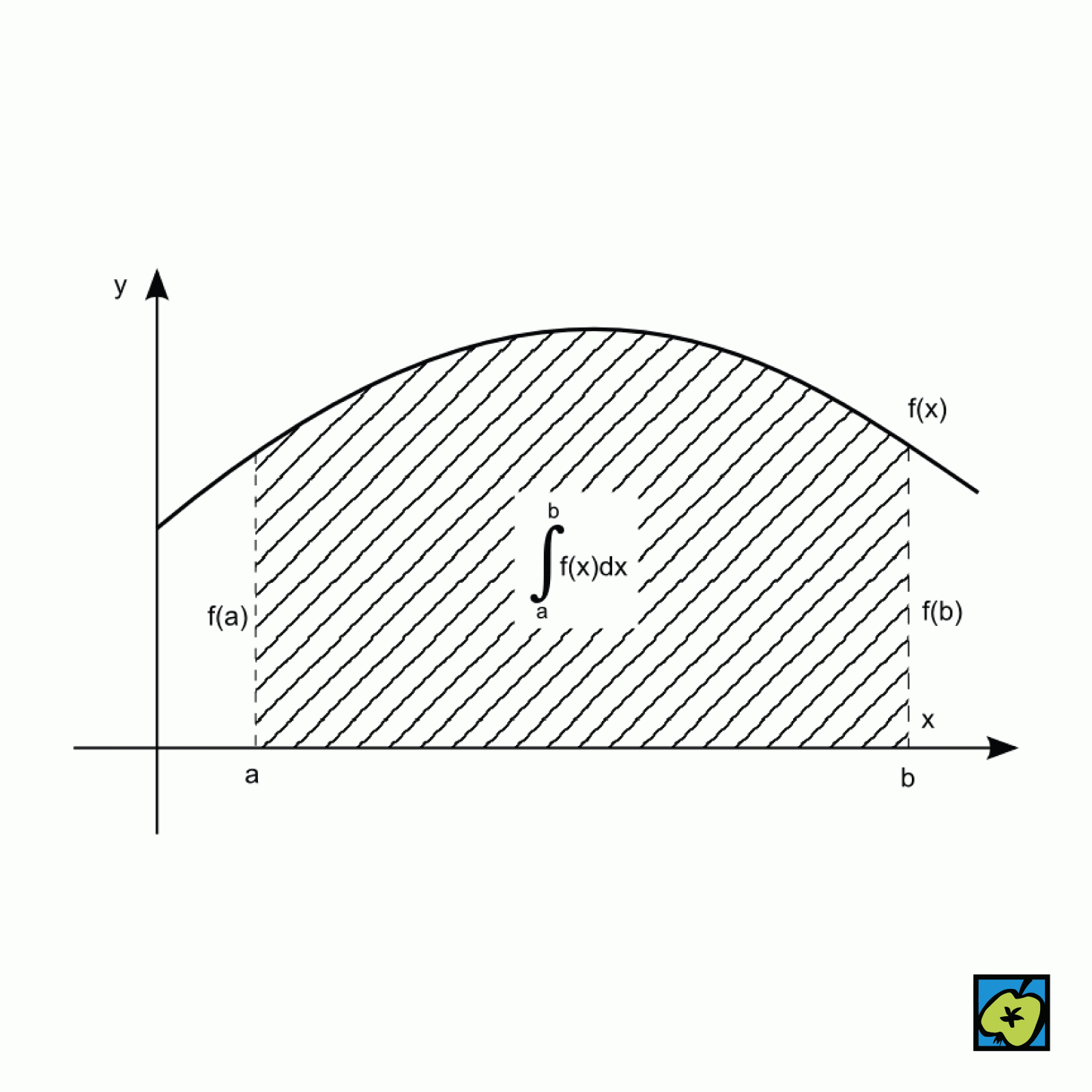
Nejjednodušším příkladem je určitý integrál funkce f v intervalu <a, b>, který je definován jako limitní hodnota součtu ploch pod grafem funkce:

\[ \int_a^b f(x) \, dx = \lim\limits_{n \to \infty} \sum_{i=1}^n f(x_i^*) \Delta x, \]

kde x_i^* je libovolný bod v dílčím intervalu a Δx je šířka tohoto intervalu. Tento součet aproximuje plochu pod křivkou f od a do b.

Neurčitý integrál funkce f je funkce F, jejíž derivace je rovna f, tj.

\[ \int f(x) \, dx = F(x) + C, \]

kde C je integrační konstanta. Významným výsledkem integrálního počtu je základní věta analýzy, která spojuje určitý a neurčitý integrál:

\[ \int_a^b f(x) \, dx = F(b) - F(a), \]

kde F je primitivní funkce k f, tj. \( F' = f \).

Integrální počet se také rozšiřuje na vícerozměrné integrály, které umožňují výpočet objemů a ploch v prostoru. Například dvojný integrál funkce f(x, y) přes oblast D je definován jako:

\[ \iint_D f(x, y) \, dA = \lim\limits_{m, n \to \infty} \sum_{i=1}^m \sum_{j=1}^n f(x_i^*, y_j^*) \Delta A, \]

kde ΔA je plocha dílčí oblasti v D.

Integrální počet má široké využití, od výpočtu ploch a objemů až po analýzu proudění tekutin a elektrických polí. V moderní matematice se pojem integrálu dále zobecňuje (např. Lebesgueův integrál), aby bylo možné pracovat s funkcemi, které nejsou spojité v tradičním smyslu.

Vytvořeno: 2. 11. 2024
Aktualizováno: 4. 11. 2024
Autor: -red-