epicykloida

Matematika / Geometrie

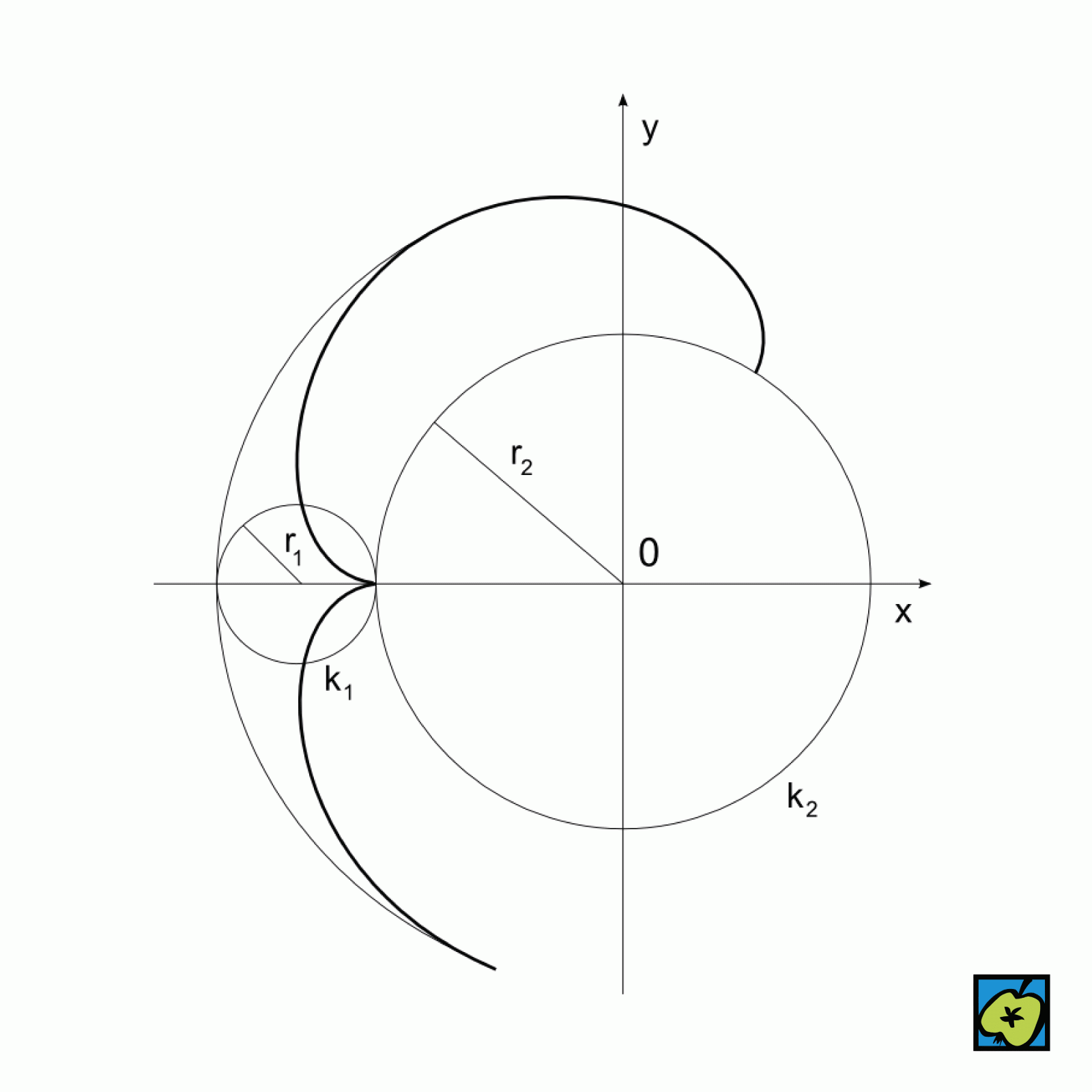
[Epicykloida, řečtina], rovinná křivka opisovaná bodem pohyblivé kružnice \(k_1\), která se beze skluzu kotálí zevně po pevné kružnici \(k_2\).

Je-li

\(r_1\) poloměr kružnice \(k_1\) , 

\(r_2\) poloměr kružnice \(k_2\),

jsou parametrické rovnice epicykloidy (s parametrem \(t\) a vhodně voleným počátečním bodem)

\(\begin{equation} x = (r_1 + r_2) \cos t - r_1 \cos \frac{r_1 + r_2}{r_1} t \end {equation}\)  ,

\(\begin{equation} y = (r_1 + r_2) \sin t - r_1 \sin \frac{r_1 + r_2}{r_1} t \end {equation}\) .

Je-li \(r_1 = r_2\), nazývá se epicykloida kardioida. Epicykloida patří k tzv. kotálnicím.

Vytvořeno: 14. 3. 2000
Aktualizováno: 6. 8. 2024
Autor: -red-

Odkazující hesla: cykloidní ozubení.