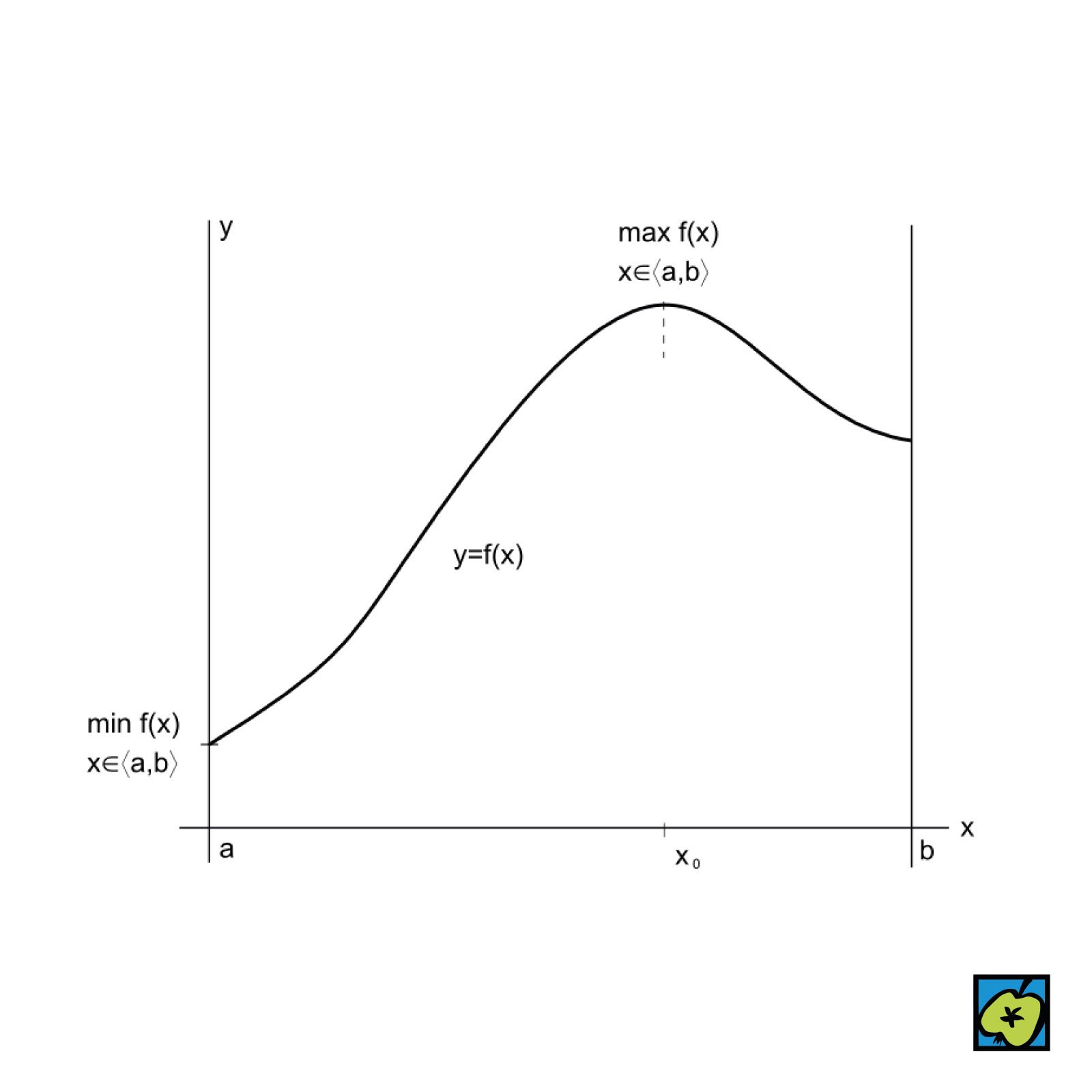
absolutní extrém

Matematika

Absolutní maximum, respektive absolutní minimum funkce \(f\) na množině \(M\), hodnota\(f(x_0),x_0\in M\), pokud existuje, pro kterou platí \(f(x)\leq f(x_0)\), resp. \(f(x)\geq f(x_0)\) pro každé \(x \in M\). Matematická značka \(\underset{x\in M} {max} f(x)\) resp. \(\underset{x\in M} {min} f(x)\), pro \(x\in M\). Ostrý absolutní extrém, ostré absolutní maximum, resp. ostré absolutní minimum, hodnota \(f(x_0),x_0\in M\), pokud existuje, pro kterou platí \(f(x)<f(x_0)\), resp. \(f(x)>f(x_0)\) pro každé \(x\in M\). Funkce nemusí mít absolutní extrém. Spojitá funkce na kompaktní množině, například na omezeném uzavřeném intervalu, nabývá svého absolutního maxima i svého absolutního minima. Místo absolutní extrém též totální extrém, globální extrém. Totéž pro maxima, minima.

Vytvořeno: 14. 3. 2000
Aktualizováno: 3. 10. 2020
Autor: -red-